안녕하세요. 주가를 분석하는 투자자 인천고래입니다.
파이썬의 rolling 함수를 통해 이동표준편차를 구하는 방법에 대해 알아보도록 하겠습니다.
우선 표준편차에 대한 이해를 하고 넘어가도록 하겠습니다.
| 목차 |
| 파이썬 - rolling 함수, 이동표준편차, 표준편차에 대한 이해 1. 표준편차 2. 이동평균 3. 이동표준편차 4. 정리 |
1. 표준편차
표준편차란 데이터가 얼마나 분산되어 있는지를 나타내는 수치입니다.
즉, 데이터가 평균에서 얼마나 떨어져 있는지를 나타내는 지표입니다.
표준편차가 작으면 데이터가 평균 주변에 모여있고, 표준편차가 크면 데이터가 넓게 흩어져 있습니다.
표준편차는 각 데이터가 평균에서 얼마나 떨어져 있는지의 차이를 제곱한 값들의 평균의 제곱근으로 계산됩니다.
이 값이 작으면 데이터가 모여 있고, 크면 데이터가 흩어져 있다는 것을 나타냅니다.
데이터 분포의 표준편차를 계산하면 해당 데이터 분포가 얼마나 일정한지, 즉 안정적인지를 평가할 수 있습니다.
또한, 표준편차는 데이터가 얼마나 분산되어 있는지를 파악하는 데에 유용합니다.
예를 들어, A 주식과 B 주식이 각각 1년 동안의 수익률이 각각 10%와 20%인 경우,
B 주식의 수익률이 A 주식의 수익률보다 높은 것은 분명하지만, B 주식의 수익률이 더 안정적인지는 표준편차를 통해 비교할 수 있습니다. 따라서, 주가 데이터의 분석에 있어서 표준편차는 매우 중요한 지표 중 하나이며, 이를 이용하여 주가 변동성을 파악할 수 있습니다.
그럼 , A주식과 B주식을 표준편차로 비교하기 위해 우선 데이터를 생성하도록 하겠습니다.
데이터는 NumPy 라이브러리를 사용해서 다음과 같이 코드를 작성하여 각 주식의 종가 데이터를 무작위로 생성할 수 있습니다.
import numpy as np
# A주식의 종가 데이터 생성
mu_a, sigma_a = 100, 10
a_closing_prices = np.random.normal(mu_a, sigma_a, 100)
# B주식의 종가 데이터 생성
mu_b, sigma_b = 100, 5
b_closing_prices = np.random.normal(mu_b, sigma_b, 100)
위 코드에서 np.random.normal 함수는 정규분포에서 무작위로 샘플링하여 데이터를 생성합니다.
각각의 주식 종가 데이터는 a_closing_prices와 b_closing_prices 변수에 저장됩니다.
이제 두 주식의 데이터를 비교하여 B주식이 더 안정적인지 알아보기 위해 표준편차를 계산해 볼 수 있습니다.
다음과 같이 코드를 작성하여 각 주식의 종가 데이터에 대한 표준편차를 계산해 보도록 하겠습니다.
# A주식의 종가 데이터에 대한 표준편차 계산
a_std = np.std(a_closing_prices)
print("A주식의 종가 데이터에 대한 표준편차:", a_std)
# B주식의 종가 데이터에 대한 표준편차 계산
b_std = np.std(b_closing_prices)
print("B주식의 종가 데이터에 대한 표준편차:", b_std)위 코드에서 np.std 함수는 주어진 데이터의 표준편차를 계산합니다.
결과적으로, A주식의 종가 데이터에 대한 표준편차와 B주식의 종가 데이터에 대한 표준편차를 비교하여 B주식이 더 안정적인지 여부를 판단할 수 있습니다.

표준편차가 높은 종목에서 투자할지 낮은 종목에서 투자할지는 여러분의 몫인 것 같습니다.

2. 이동평균
이동표준편차에 대해 알아보도록 하겠습니다.
이동평균이 시계열 데이터를 부드럽게 만들어 주는 데 유용하다는 것을 이미 알고 계실 것입니다.
이동표준편차(rolling standard deviation)는 마찬가지로 시계열 데이터를 부드럽게 만들어 주면서 통계적인 특징을 파악하는 데 유용한 기법입니다.
이동평균과 같이 일정 기간 동안의 데이터를 기반으로 계산하는 것이 특징입니다.
이동표준편차는 각각의 시점에서 일정한 기간 동안의 데이터들의 표준편차를 구하는 것입니다.
예를 들어, 20일 동안의 종가 데이터의 이동표준편차를 계산하는 경우, 각각의 시점에서 20일치의 종가 데이터를 기반으로 표준편차를 계산합니다. 이렇게 하면 특정 시점에서 그 시점을 기준으로 한 기간 동안의 변동성을 파악할 수 있습니다.
파이썬에서 이동표준편차를 계산하기 위해서는 pandas의 rolling 함수를 이용하면 됩니다.
rolling 함수는 일정한 기간 동안의 데이터를 묶어서 적용할 함수를 지정하는 함수입니다.
예를 들어, rolling 함수를 이용해 이동평균을 계산하는 경우 다음과 같은 코드를 사용할 수 있습니다.
import pandas as pd
# 데이터프레임 생성
df = pd.DataFrame({'value': [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]})
# 이동평균 계산
ma = df['value'].rolling(window=3).mean()
print(ma)위 코드에서 window 인자를 이용해 계산하고자 하는 기간을 설정할 수 있습니다.
이렇게 계산한 이동평균은 다음과 같습니다.
0 NaN
1 NaN
2 2.0
3 3.0
4 4.0
5 5.0
6 6.0
7 7.0
8 8.0
9 9.0
Name: value, dtype: float64이동표준편차도 이와 비슷한 방법으로 계산할 수 있습니다.
다음은 주식 종가 데이터에서 20일간의 이동표준편차를 계산하는 코드입니다.
3. 이동표준편차
주식 종가 데이터로 20일간의 이동표준편차를 계산하는 파이썬 코드는 다음과 같습니다.
import pandas as pd
# CSV 파일 로드
df = pd.read_excel('비트나인.xlsx')
# 종가 데이터만 추출한다.
close = df['Close']
# 20일 이동평균 계산
ma20 = close.rolling(window=20).mean()
# 20일 이동표준편차 계산
std20 = close.rolling(window=20).std()
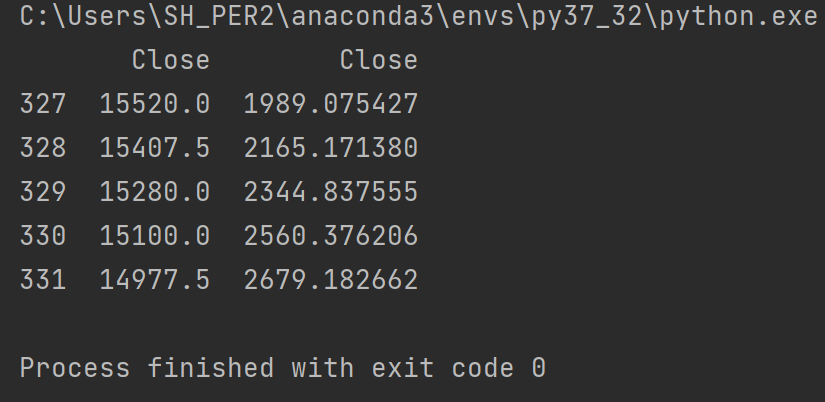
# 마지막 5개 데이터만 출력해 비교
print(pd.concat([ma20, std20], axis=1).tail(5))위 코드에서는 pandas 라이브러리의 read_excel 함수를 사용하여 xlsx 파일을 로드합니다.
로드한 데이터프레임에서는 rolling 함수를 사용하여 20일간의 이동평균과 이동표준편차를 계산합니다.
rolling 함수의 window 파라미터는 이동평균 또는 이동표준편차를 구하는 기간을 20으로 설정했습니다.
마지막으로 계산한 이동평균과 이동표준편차를 출력하면 됩니다.
아래는 결과 이미지입니다.
4. 정리
rolling.std() 함수와 np.std() 함수의 차이점이 무엇인지? 그리고 어떨 때 사용을 해야 할지 구분이 잘 안 되실 수 있을 것 같습니다.
차이점은 다음과 같습니다.
rolling.std() 함수는 Pandas에서 제공하는 rolling 함수를 사용하여 이동 표준편차를 계산하는 함수입니다.
이동 표준편차는 주어진 기간의 표준편차를 계산하는 것이며, 이동평균과 함께 사용하여 주가의 변동성을 분석하는 데 많이 사용됩니다.
np.std() 함수는 NumPy에서 제공하는 표준편차 함수입니다. 이 함수는 주어진 데이터의 표준편차를 계산하는 것이며, 주로 데이터의 분포를 나타내는 지표로 사용됩니다.
따라서, 이동 표준편차를 계산할 때는 rolling.std() 함수를 사용하고,
일반적인 표준편차를 계산할 때는 np.std() 함수를 사용하는 것이 좋습니다.
이것으로 rolling의 이동표준편차에 대한 글을 마치도록 하겠습니다.
오늘도 제 글을 읽어주신 모든 분들께 감사의 말씀을 드립니다. 감사합니다.
'Quant Stock' 카테고리의 다른 글
| 파이썬 - 스토캐스틱(Stochastic Oscillator)이해와 차트 만들기 (0) | 2023.03.20 |
|---|---|
| 파이썬 - RSI(Relative Strength Index, 상대강도지수) 차트 만들기 (0) | 2023.03.19 |
| 파이썬 - 이동평균선 차트 만들기 (plt.axes에 대한 설명 포함) (0) | 2023.03.19 |
| 엔벨로프 차트 만들기 - 파이썬 코드 (LG전자 데이터 가져오기, FinanceDataReader) (0) | 2023.03.17 |
| 볼린져밴드의 이해 - 파이썬 코드 (비트나인.xlsx 데이터) (0) | 2023.03.14 |




댓글